Order out of disorder
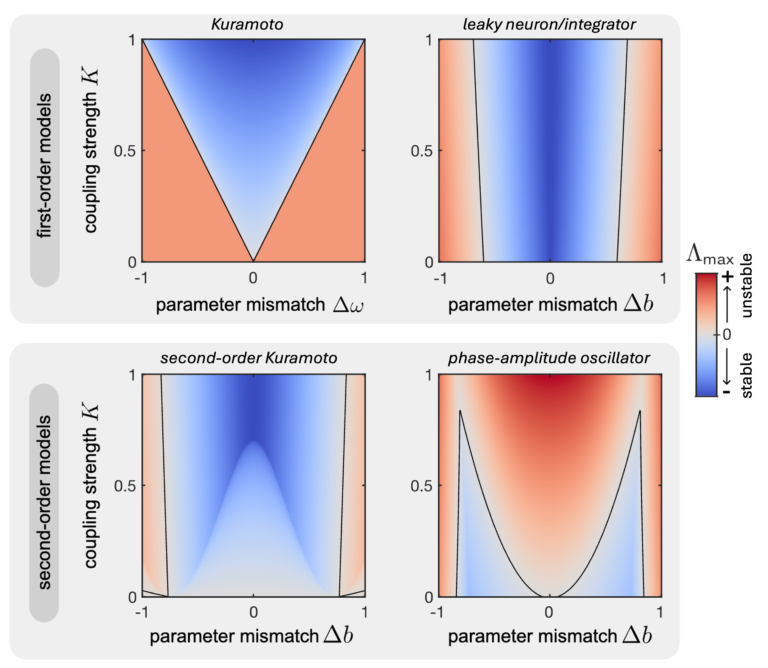
My recent research shows that disorder can promote, rather than inhibit, stable collective states—such as synchronization patterns, memory states, and consensus formation—across a broad class of dynamical systems, including those relevant to unconventional computing. Unlike the classical view from first-order models (e.g., Kuramoto), which suggests disorder disrupts spatiotemporal organization, I show that richer systems with non-Hermitian Jacobians—arising from second-order equations of motion or phase-amplitude coupling—can harness disorder to enhance stability.
This opens new directions for designing neurocomputing architectures that achieve faster convergence, stronger resilience, and improved performance across a broad range of computational tasks.
Designing oscillator machines for large-scale combinatorial optimization
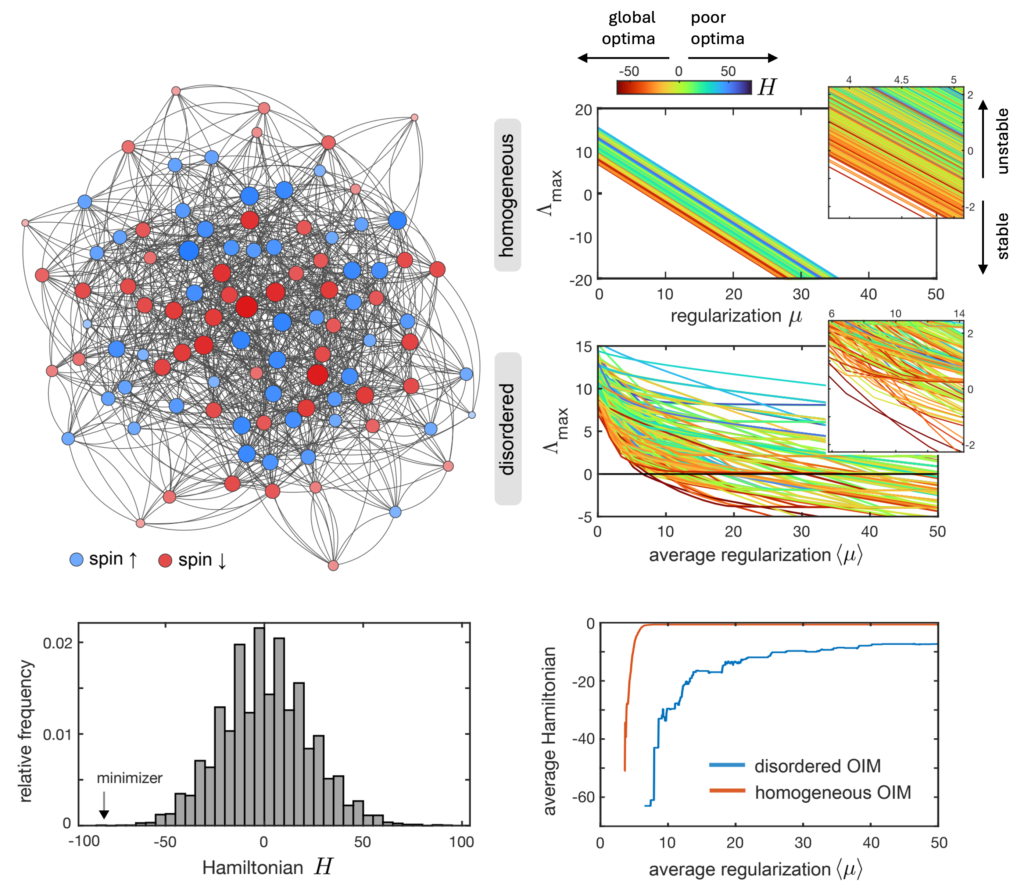
Coupled electronic oscillators known as oscillator Ising machines (OIMs) offer a powerful analog, energy-efficient hardware for solving combinatorial optimization problems used in areas like circuit design and logistics, from MaxCut to the traveling salesman. Here, we intentionally introduce disorder into the oscillators’ harmonic signals in order to bias the circuit convergence towards global minimizers. Our work also lays down the theory for the convergence and stability of OIMs in random graphs.
See more:
A Allibhoy, AN Montanari, F Pasqualetti, AE Motter. Global optimization through heterogeneous oscillator Ising machines. Proceedings of the Conference on Decision and Control (2025, to appear).
Optimal flocking of drone swarms, from target tracking to obstacle avoidance
Inter-individual differences are often viewed as obstacles to flocking and coordination. Yet, our work shows that tuning heterogeneity in agent parameters can lead to faster and more robust flocking, even in the presence of communication delays or complex tasks. These include drones navigating unmapped environments, tracking unpredictable targets, or drawing pictures in the sky (see video).
In nature, the coordination and decision-making of animal groups can be viewed as forms of distributed computation. Flocks of starlings, for example, can react to predators up to 10 times faster than isolated individuals. Growing evidence suggests that consistent differences in “animal personalities” and phenotypic variation are not just noise, but fundamental evolutionary drivers of collective function. Our research builds directly on this insight, showing how agent heterogeneity can enhance coordination in both biological and engineered systems.
See more:
AN Montanari, AED Barioni, C Duan, AE Motter. Optimal flock formation induced by agent heterogeneity. Nature Communications, in press (2025).
Scaling coupled laser arrays for high-power photonics, data processing, and coherent computation
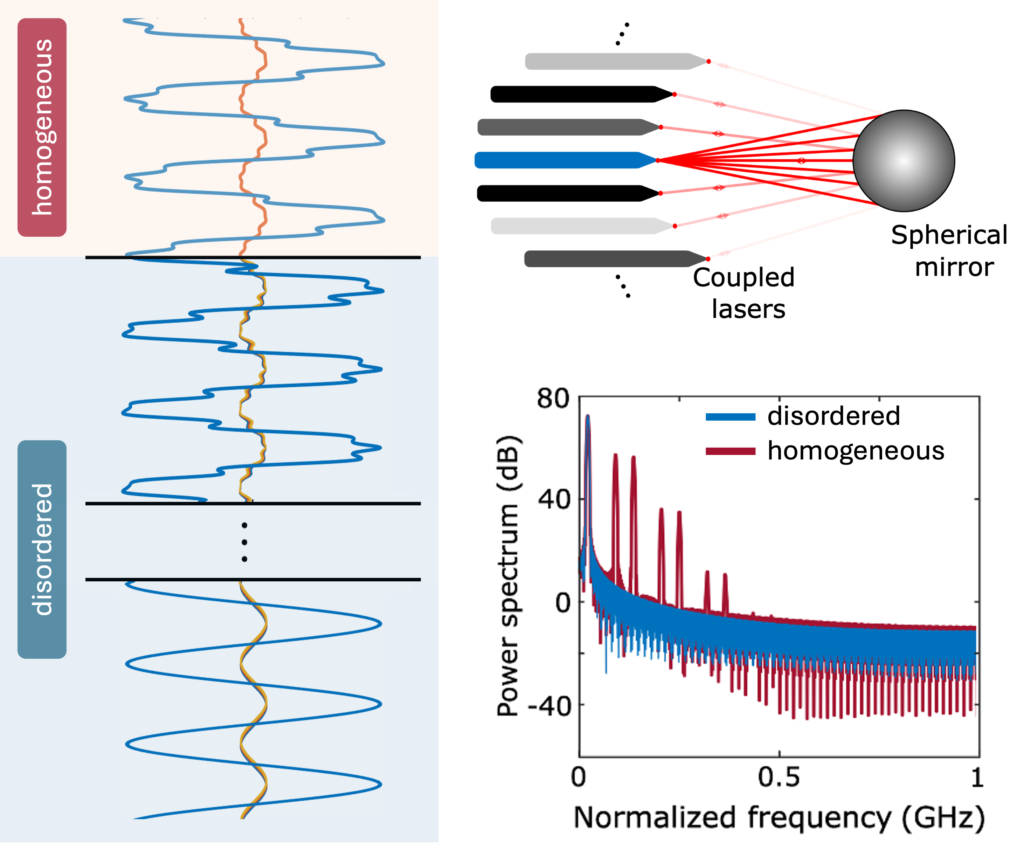
Coupled semiconductor lasers are a scalable route to high-power photonics in the THz gap, but synchronizing large arrays is notoriously difficult due to delays and instabilities. In our work, we show that controlled levels of disorder into the lasers’ constructive parameters can stabilize synchronization across up to a thousand units, generating combined beams with sharper frequency spectra, stronger phase coherence, and a 1000-fold higher power output.
These findings open opportunities for both next-generation laser technologies and neuromorphic architectures that rely on coherent laser sources, from high-precision spectroscopy and LiDAR sensing to photonic neural networks.
See more:
AED Barioni, AN Montanari, AE Motter. Interpretable disorder-promoted synchronization and coherence in coupled laser networks. Physical Review Letters, in press (2025).
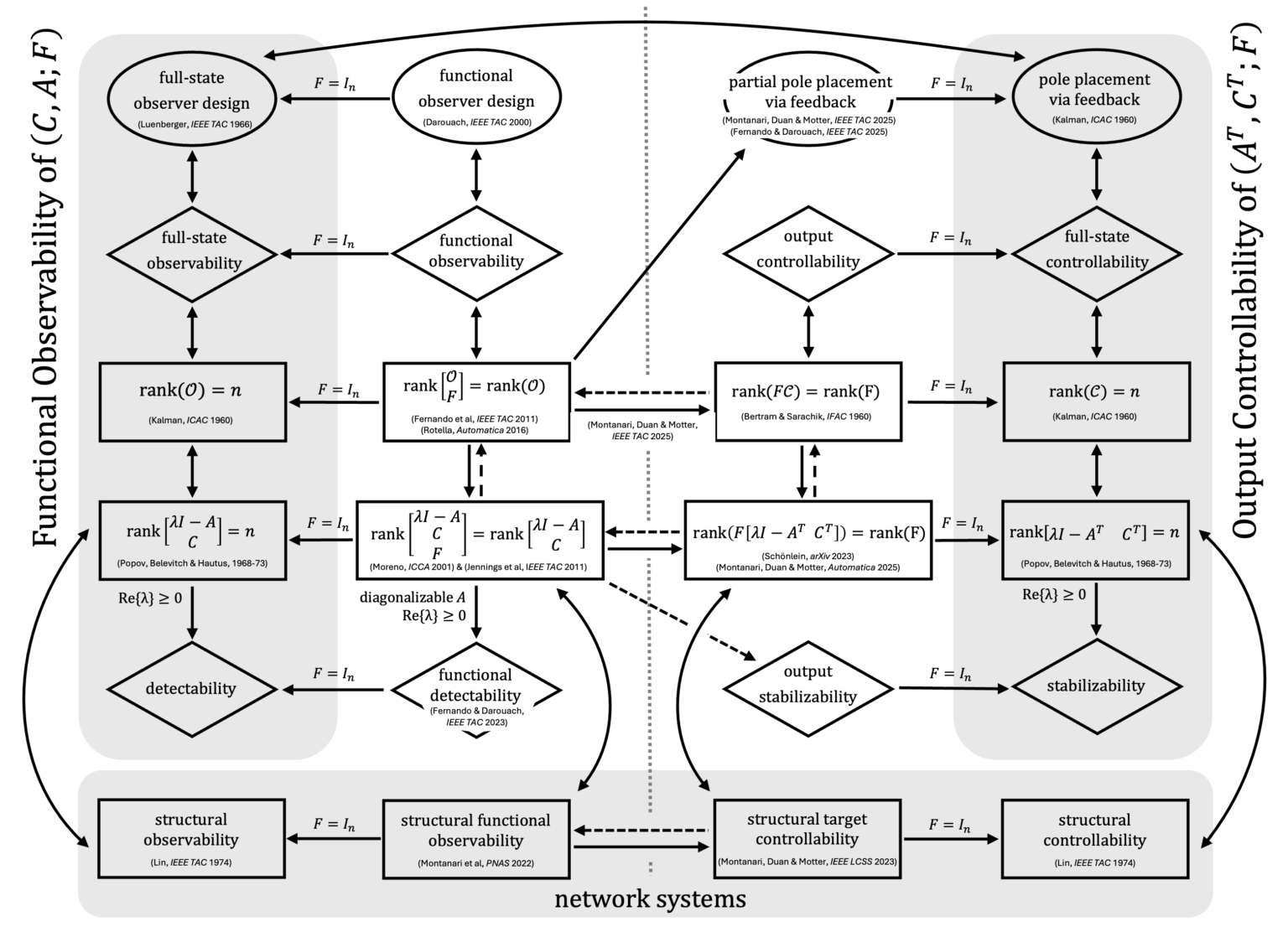
Mapping the theory of control for (partial) state control and estimation
Technological, computing, and infrastructure systems have grown dramatically in scale and complexity over the past decades. Yet, modern control theory has been developed primarily for small, low-dimensional systems, where full control and monitoring are often available by design (think of aircrafts, chemical reactors, and robotics). By contrast, large-scale network systems—like power grids, autonomous vehicle fleets, and high-performance computing clusters—lack full measurement access, global communication interfaces, and centralized control architectures. To cope with the high dimensionality of modern network systems, we must extend classical theory to function under limited access to system states.
When the objective is to control or estimate only a targeted subset (or a low-dimensional functional) of state variables, the notions of target controllability and functional observability provide the right framework. My research has uncovered the conditions under which these notions become dual, linking results that were established in control theory 50 years apart. As a result, methods developed for one problem can now be translated to another, leading to the discovery of new efficient algorithms for optimal sensor/driver placement, data-driven controllers/observers design, and nonlinear analysis.
Selected publications:
AN Montanari, C. Duan, AE Motter. Duality between controllability and observability for target control and estimation in networks. IEEE Transactions on Automatic Control, 70:5584-5591 (2025).
AN Montanari, C Duan, AE Motter. On the Popov-Belevitch-Hautus tests for functional observability and output controllability. Automatica, 174:112122 (2025).
AN Montanari, C Duan, LA Aguirre, AE Motter. Functional observability and target state estimation in large-scale networks. Proceedings of the National Academy of Sciences of the U.S.A., 119: e2113750119 (2022).
Scalable approaches for large-scale complex networks
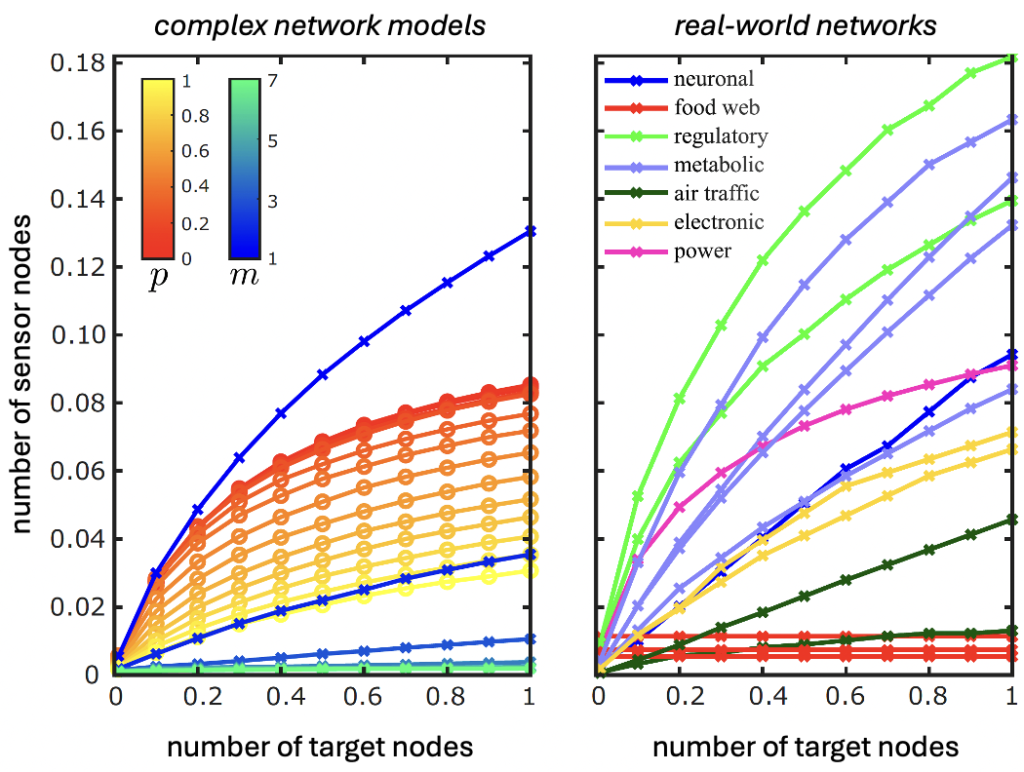
Many high-dimensional systems are described by networks, including neural networks, power grids, traffic systems, biological regulatory networks, and food webs. It is therefore essential to develop control analysis and techniques tailored to such systems, making use of their graph properties—for example, connected components, paths between nodes, and “dilations.” This research establishes graph-theoretical conditions for the estimation and control of a target subset of nodes, without requiring full system observability or controllability. Building on this theory, we develop highly scalable algorithms for the optimal placement of sensors/actuators in a network, as well as the design of state observers/controllers.
See more:
AN Montanari, C Duan, LA Aguirre, AE Motter. Functional observability and target state estimation in large-scale networks. Proceedings of the National Academy of Sciences of the U.S.A., 119: e2113750119 (2022).
AN Montanari, C Duan, AE Motter. Target controllability and target observability of structured network systems. IEEE Control Systems Letters, 7:3060-3065 (2023).
AN Montanari, LA Aguirre. Observability of network systems: A critical review of recent results. Journal of Control, Automation and Electrical Systems, 31:1348-1374 (2020).
Nonlinear analysis tools, from chaotic attractor reconstruction to early-warning signals
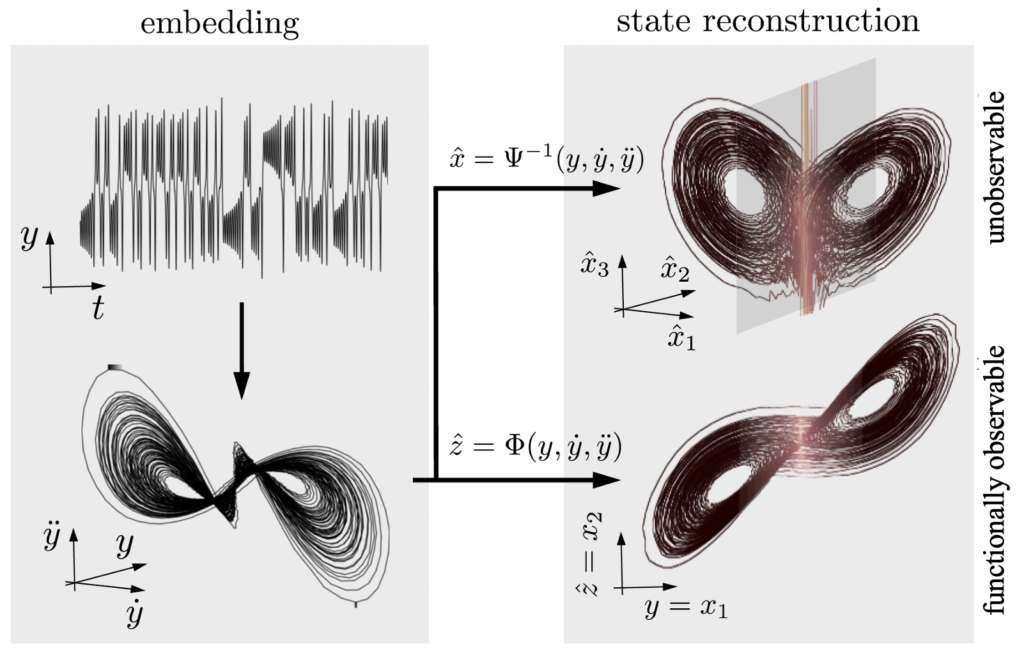
What can be and cannot be reconstructed from limited data, and how this shapes our predictions of the future, is the major question answered here. My research has developed the observability theory for nonlinear dynamical systems, allowing us to identify which state variables can be reliably reconstructed from data (using, for example, time-delay embeddings or Kalman/particle filters) and to assess how transients and chaotic regimes can locally affect this reconstruction. This work provides a deeper understanding of how several data-driven nonlinear analysis tools perform in practice, with applications ranging from paleoclimate reconstruction to early-warning signals of critical transitions (e.g., in epilepsy and cell regulation).
See more:
AN Montanari, L Freitas, D Proverbio, J Gonçalves. Functional observability and subspace reconstruction in nonlinear systems. Physical Review Research, 4:043195 (2022).
D Proverbio, AN Montanari, A Skupin, J Gonçalves. Buffering variability in cell regulation motifs close to criticality. Physical Review E, 106:L032402 (2022).
LL Portes, AN Montanari, D Correa, M Small, LA Aguirre. The observability properties of the recorded time series influence the reliability of recurrence network analysis. Chaos, 29:083101 (2019).
AN Montanari, LA Aguirre. Particle filtering of dynamical networks: Highlighting observability issues.
Chaos, 29:033118 (2019).
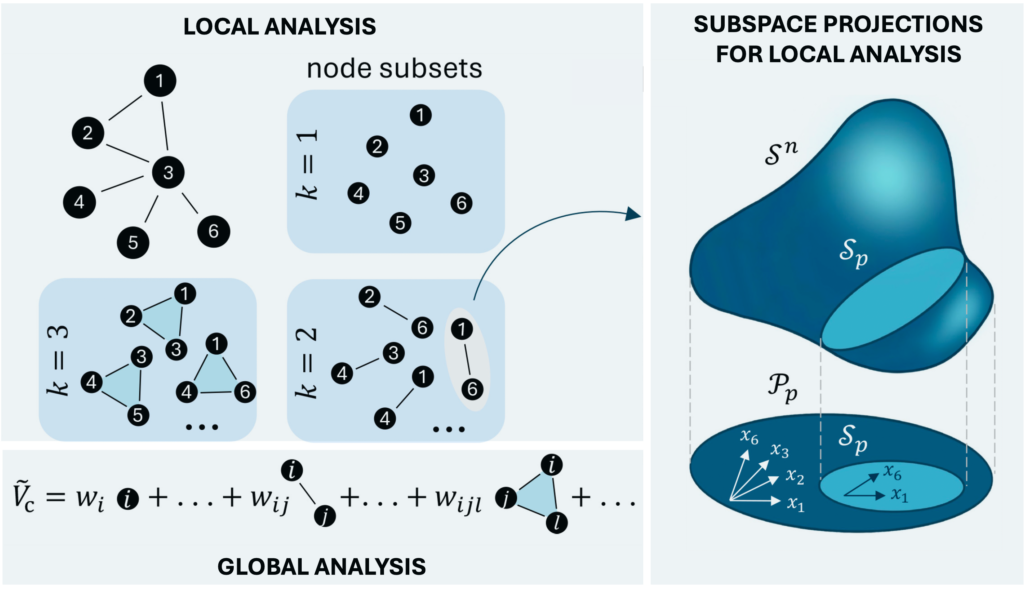
Distributed methods for global stability analysis
Even after 130 years since their formulation, Lyapunov functions remain the primary tool for stability analysis. They allow us to quantify the resilience and stability margins of a system under perturbations (through estimates of its basin of attraction) and to design feedback controllers for nonlinear dynamics. However, these functions are notoriously hard to derive analytically, and most computational methods (like SOS optimization) struggle to infer Lyapunov functions for systems with more than a dozen state variables.
To overcome these issues, we developed a distributed approach for constructing Lyapunov functions for high-dimensional network systems. By decomposing the problem into multiple low-dimensional subproblems that rely only on local network information, this method leverages parallel computation to scale efficiently for systems with hundreds of state variables. We are now extending these techniques to applications in diverse domains, ranging from the vulnerability analysis of the UK power system to the study of adversarial attacks in neural networks.
See more:
Y Wang, AN Montanari, AE Motter. Distributed Lyapunov functions for nonlinear networks. IEEE Control Systems Letters, 9:486-491(2025)
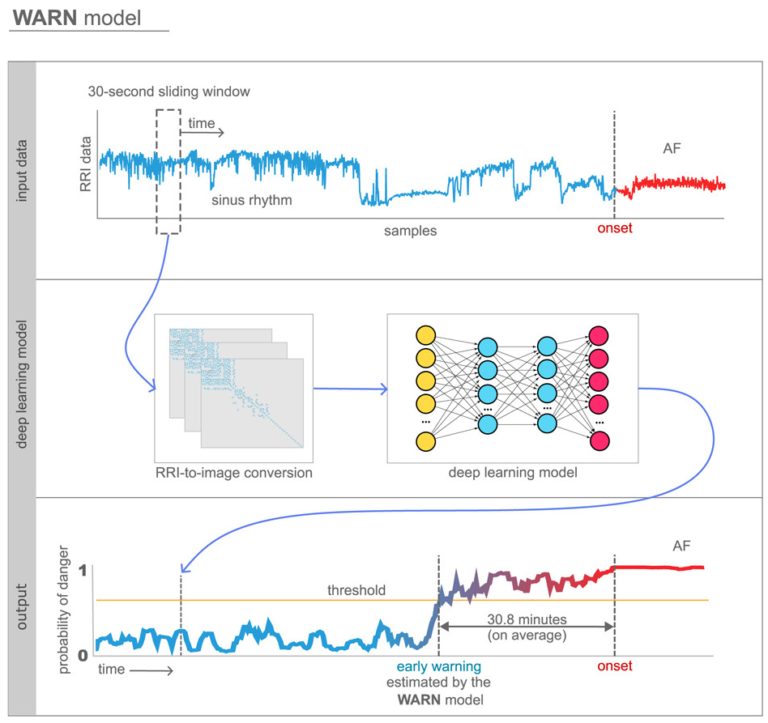
Deep learning for predicting and diagnosing medical conditions
My research uses AI models, such as deep convolutional neural networks, to predict and infer medical conditions from biomedical data. Recent work shows that our models can predict atrial fibrillation—the most common cardiac arrhythmia—up to 30 minutes in advance using real-time data from wearable devices like smartwatches (see video for a representative patient). These models have also been applied to diagnose sleep apnea from commonly available wearables, and we are currently working on expanding this line of research to advance AI-driven methods for personalized healthcare, allowing for earlier interventions, more accessible diagnostics, and reduced healthcare costs.
Research articles:
ME Gavidia, H Zhu, AN Montanari, J Fuentes, …, X He, X Yang, J Gonçalves. Early warning of atrial fibrillation using deep learning. Patterns, 5:100970 (2024).
G Retamales, ME Gavidia, B Bausch, AN Montanari, A Husch, J Gonçalves. Towards automatic home-based sleep apnea estimation using deep learning. npj Digital Medicine, 7:144 (2024).
Media and editorial coverage:
SF Friedman, S Khurshi. Consider this a WARNing. Patterns, 5:101009 (2024).
C Pelc. Wearable tech uses AI to detect cardiac arrhythmia 30 minutes before onset. Medical News Today (May, 2024).
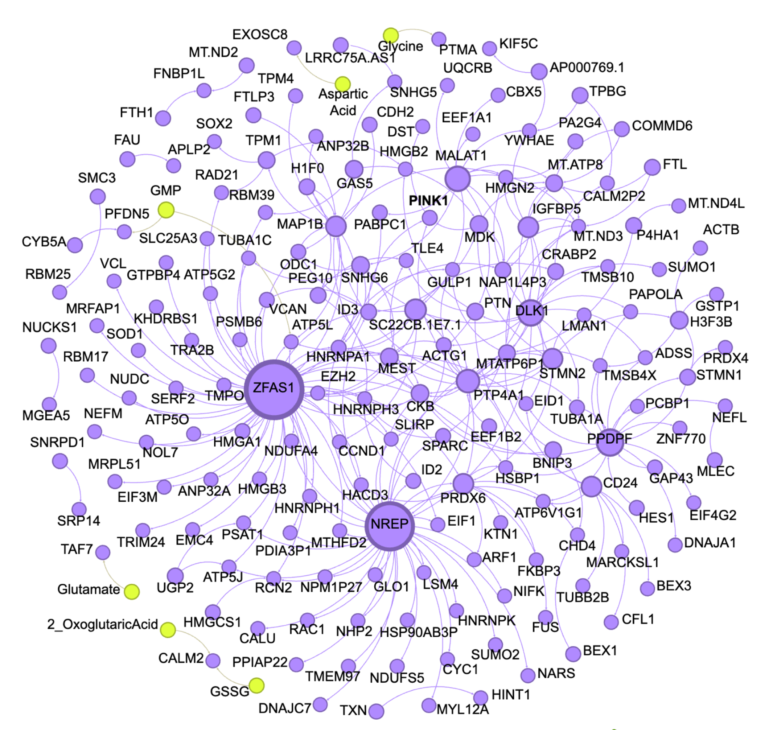
Inferring regulatory networks for drug discovery and disease modeling
In living systems, cellular function is regulated by molecular interactions spanning multiple spatial and temporal scales, from the transcriptome (gene expression) and proteome (protein signaling and structure) to the metabolome (energy and chemical fluxes).
We developed the first method for the inference of biological regulatory networks from multi-omic data. Our approach is unique in two key ways: 1) it uses time-series molecular data, allowing for the inference of causal interactions among biomolecules, rather than simple correlations, and 2) it identifies both inter- and intra-omic molecular interactions, allowing for the discovery of regulatory links among genes, proteins, and metabolites. Our results show that uncovering pathways across these scales can guide drug target discovery and help bridge the genotype-phenotype gap in complex diseases like Parkinson’s.
At its core, the mathematics are based on differential-algebraic equations, which come with their own challenges for identifiability and method development but also opportunities for the discovery of mechanisms across timescales.
See more:
MM Garcia, A Aalto, AN Montanari, A Skupin, J Gonçalves. Multi-omic network inference from time-series data. npj Systems Biology and Applications 11:114 (2025).
M Jayadharan, C Catlett, AN Montanari, NM Mangan. SODAs: Sparse optimization for the discovery of differential and algebraic equations. arXiv:2503.05993 (2024).
AN Montanari, F Lamoline, R Bereza, J Gonçalves. Identifiability of differential-algebraic systems. arXiv:2405.13818 (2024).
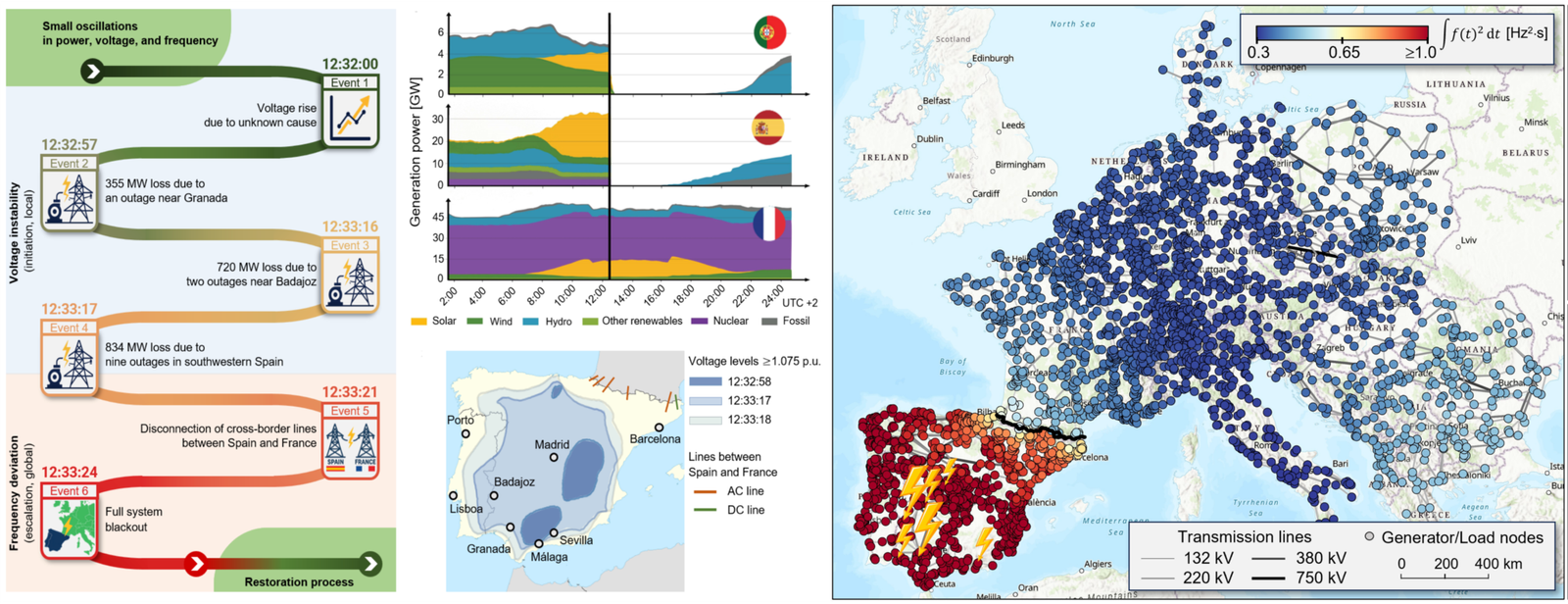
Cascading failures, renewable penetration, and the Iberian blackout
On April 28, 2025, the Iberian Peninsula faced one of the largest blackouts in history, leaving more than 50 million people without electricity for over 16 hours. Official reports by the transmission system operators identified voltage instabilities as the main culprit for the initial generation loss. Yet, our analysis reveals that loss of synchronism caused by frequency disturbances played a major role in the rapid, wide-area propagation of the cascade. Crucially, the fast spread of disturbances within the Iberian Peninsula (compared to other regions like France) is a direct result of its lack of inertia due to high-renewable penetration.
Over the past few years, renewables have been implicated in an increasing number of blackouts around the world and are, therefore, under intense scrutiny. Our study of the Iberian blackout points out that investment towards the coordinated modernization of renewable generation and transmission infrastructure is not only necessary to fulfill the renewables’ core promise of clean energy, but also an opportunity to strengthen grid resilience.
See more on the Iberian blackout:
Y Wang, AN Montanari, AE Motter. Rethinking the green power grid: Renewables for stability, not just for climate. Under review (2025).
Y Wang, AN Montanari, AE Motter. Nonnormal frequency dynamics under high-renewable penetration: A case study of the Iberian blackout. Under review (2025).
Further research on power-grid dynamics, synchronization, and cyber-attack detection:
AN Montanari, C Duan, LA Aguirre, AE Motter. Functional observability and target state estimation in large-scale networks. Proceedings of the National Academy of Sciences of the U.S.A., 119: e2113750119 (2022).
AN Montanari, EI Moreira, LA Aguirre. Effects of network heterogeneity and tripping time on the basin stability of power systems. Communications in Nonlinear Science and Numerical Simulation, 89:105296 (2020).
AN Montanari, L Freitas, LAB Torres, LA Aguirre. Phase synchronization analysis of bridge oscillators between clustered networks. Nonlinear Dynamics, 97:2399-2411 (2019).